Lifting topological codes:
Single-shot codes from topological order
Jacob Bridgeman, Aleks Kubica, and Mike Vasmer

arXiv:2305.06365

EQUS — Sydney University, October 2023
Overview

  1. Main idea

  2. Subsystem codes

  3. Single-shot QEC

  4. Gauge color codes

  5. Subsystem toric code

  6. Subsystem abelian quantum double codes

  7. Summary

Main idea
  • Use 2D topological codes + 3D geometry to construct 3D subsystem codes with single-shot QEC
Subsystem codes

All stabilizer codes are subsystem codes ()

Pauli subsystem codes:

  • : Gauge group (nonabelian)

  • : Stabilizer group

Examples:
  • Bacon-Shor code
  • Gauge color code
  • Subsystem toric code

Given a stabilizer code, add some logical pairs to to get a subsystem code

Subsystem codes | ⟦4,2,2⟧ ⟶ ⟦4,1,2⟧

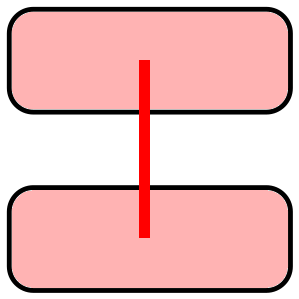
⟦4,2,2⟧ stabilizer code:

 , 

Two logical qubits:

        

⟦4,1,2⟧ subsystem code:

 ,   ,   , 

Subsystem codes | Why?

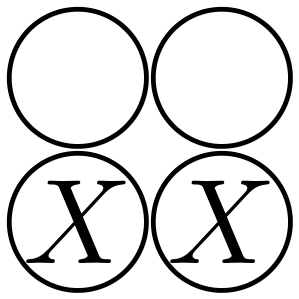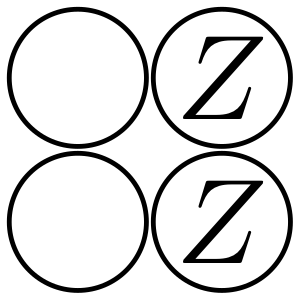
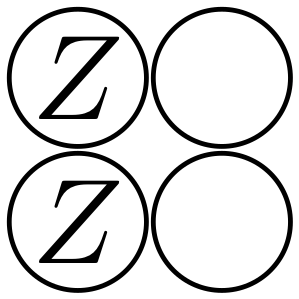  • Lower weight check operators

  • More fault-tolerant logical gates

  • More general formalism – Possibility for novel codes

  • Single-shot QEC

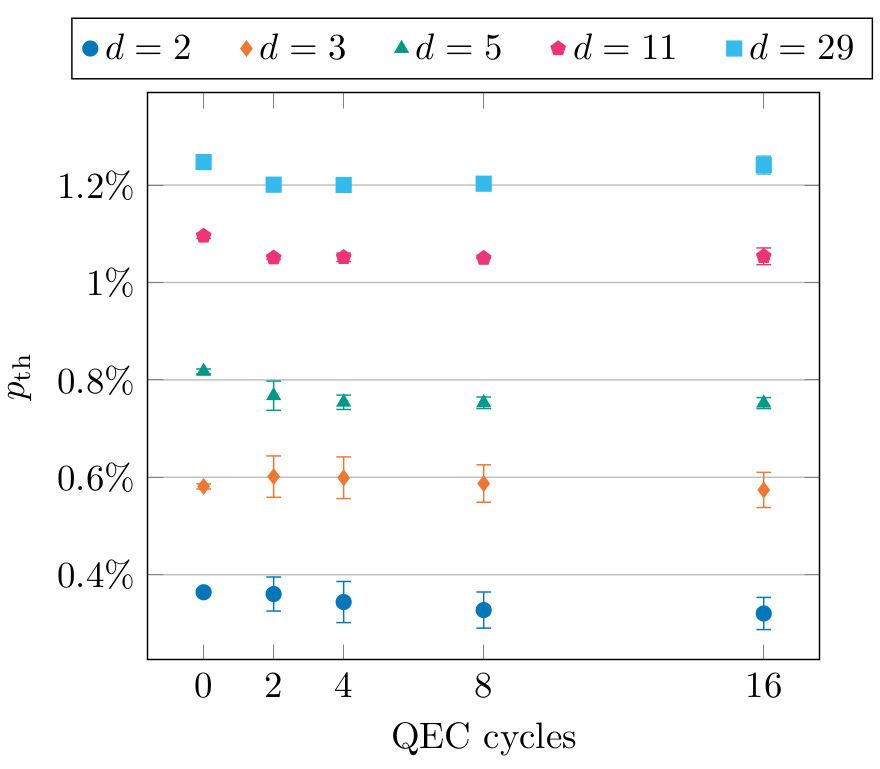
Single-shot QEC

  • Bombin | arXiv:1404.5504

  • Single-shot QEC: correct errors in a single round of syndrome measurement

    • Even with measurement errors
Gauge color codes

  • 3 (space) dimensional subsystem codes

  • Defined on 4-colorable lattices

  • Gauge operators defined on 2D faces

  • Stabilizer operators associated to volumes

Gauge color codes | Gauge flux
  • Non-abelian gauge group gauge measurement outcomes are random
  • Gauge flux is the pattern of outcomes
  • Although outcomes are locally random, they are correlated
    • Product of gauge flux at a stabilizer must be
    • There may be other constraints
⟦4,1,2⟧ Code | Gauge flux

⟦4,1,2⟧ subsystem code:

 ,   ,   , 

 , 

       
Gauge flux | Measurement errors

 ,   ,   , 

 , 

                           

                 
Gauge color codes | Observations

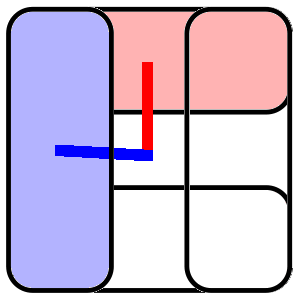
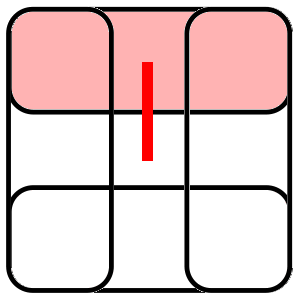
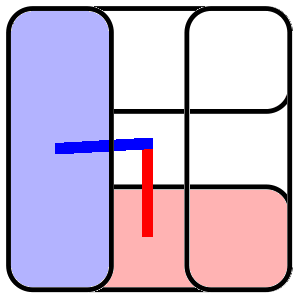
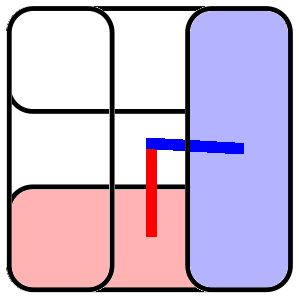
  • Each volume forms a 2D stabilizer color code
  • Qubits are shared between neighboring codes
  • Each stabilizer can be reconstructed in 3 ways – redundancy
  • Gauge fluxes can be interpreted as anyons on the 2D color codes
  • Net neutral charge on sphere Gauss law for gauge flux
Subsystem toric code
  • Introduced in arXiv:2106.02621
  • More elementary than gauge color code
  • Separates stabilizer constraints from topological constraints (Gauss law)
  • Gauge operators associated to 2D faces and vertices
Subsystem toric code | Stabilizers

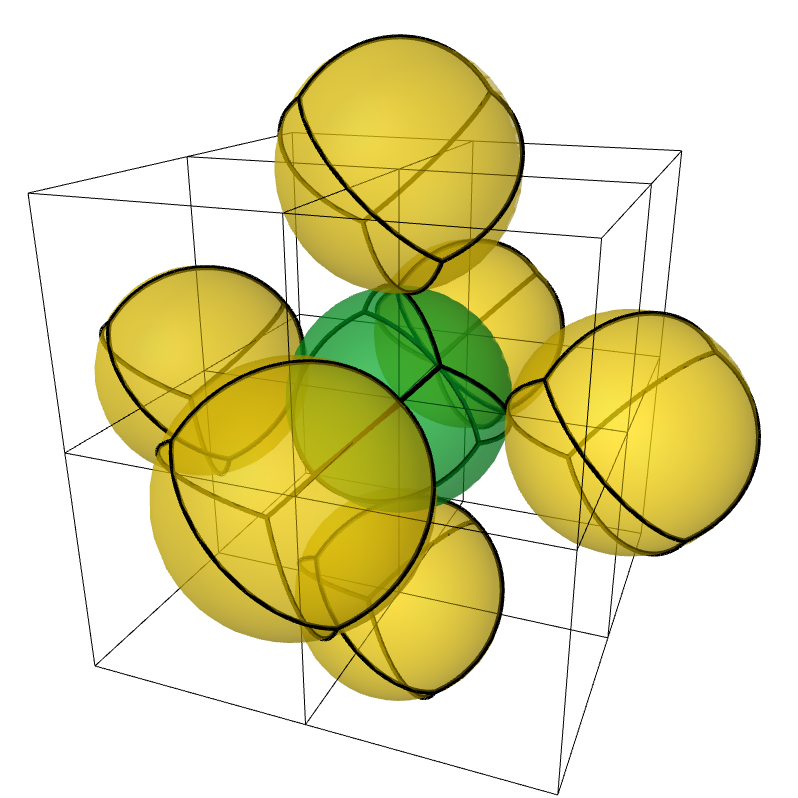
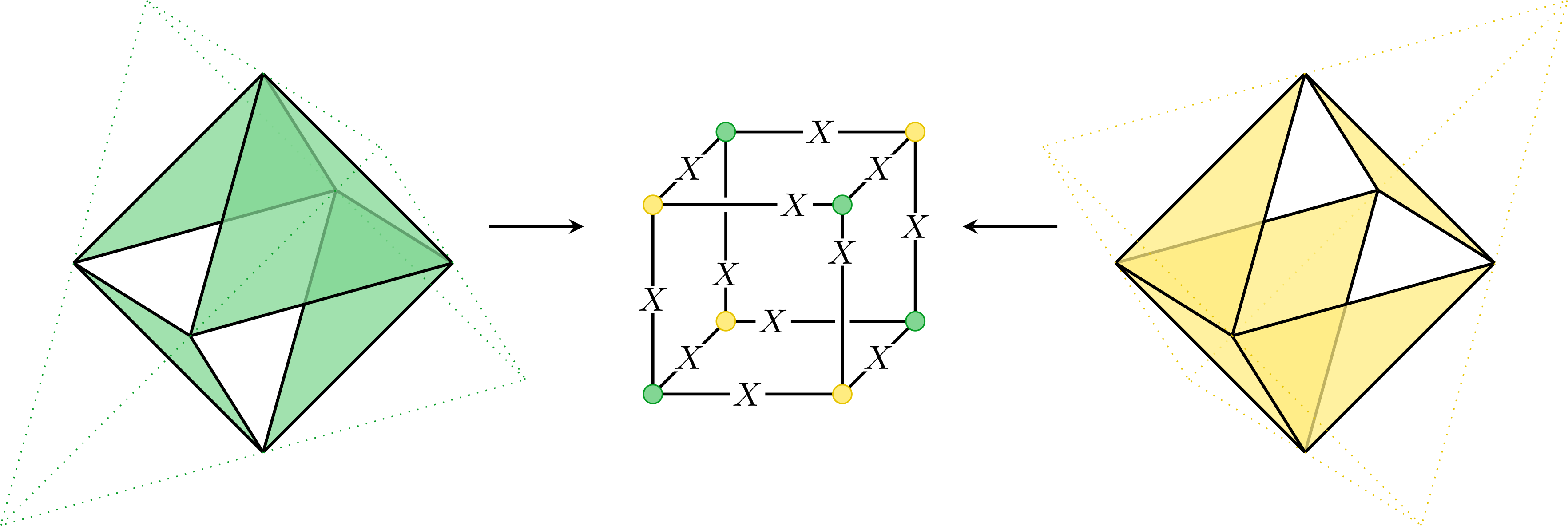
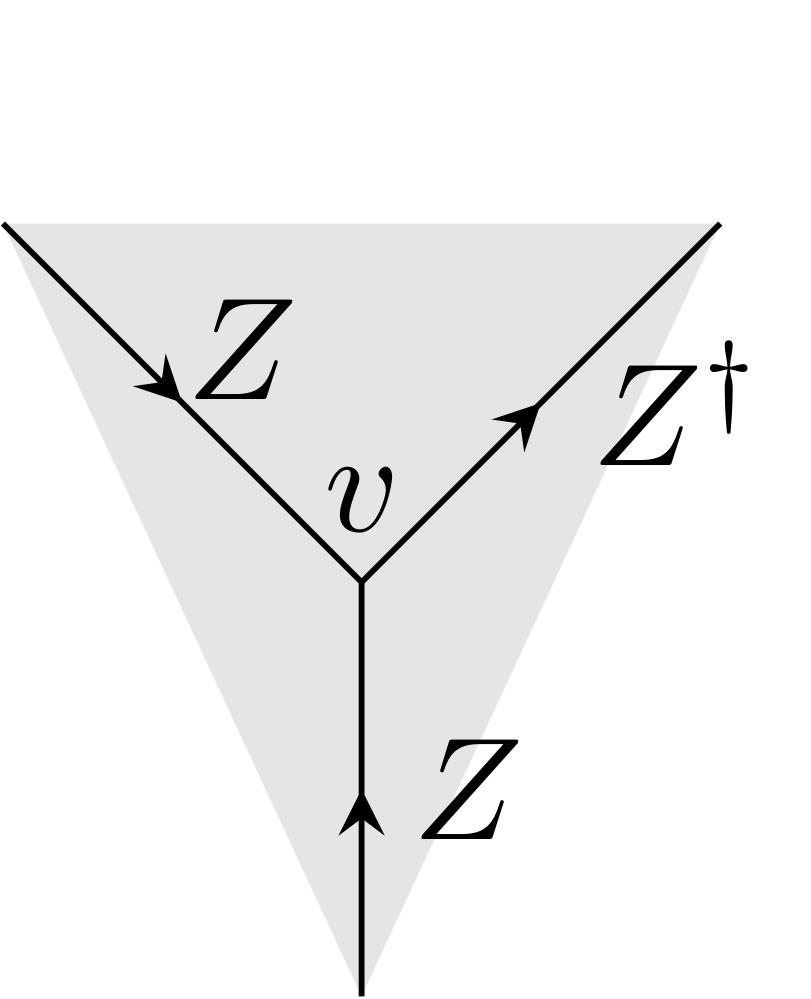
  • Associated to volumes of the lattice

  • Each stabilizer can be reconstructed in 2 ways – from only green or only yellow gauge operators

Subsystem abelian quantum double code

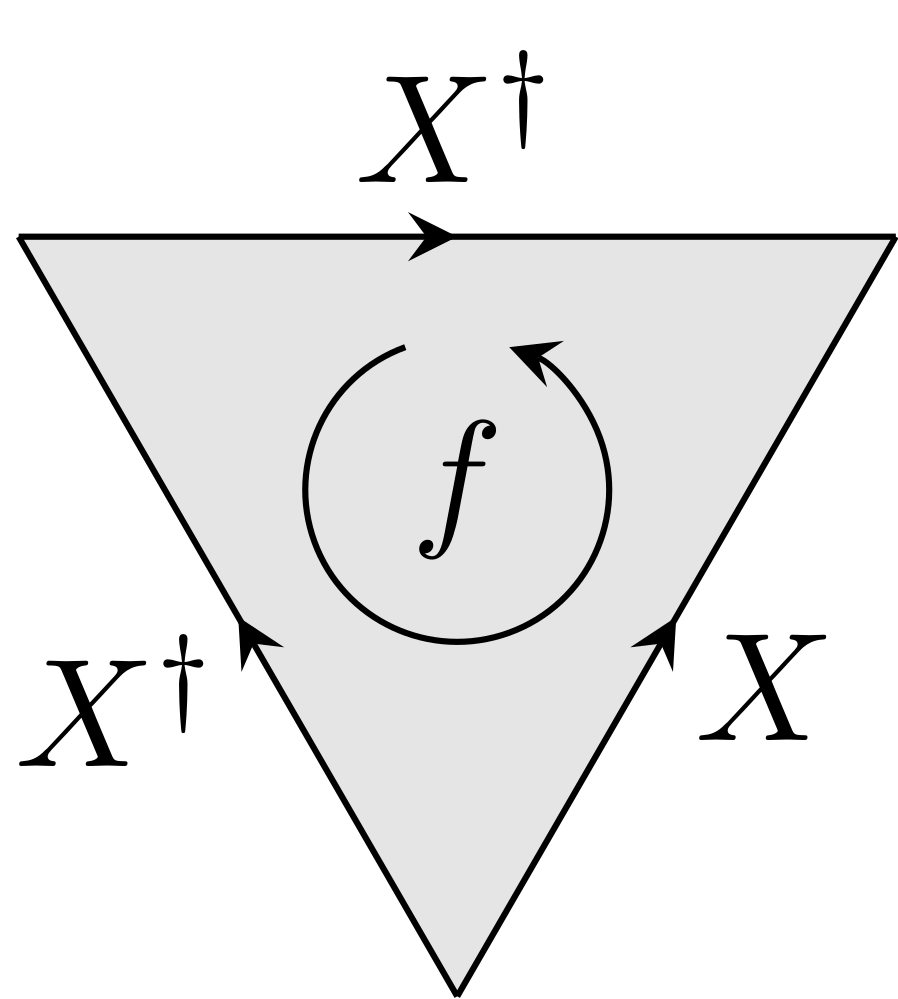
  • Instead of (toric code), use

  • and type anyon fusion rules dictate gauge flux Gauss law

Subsystem abelian quantum double code | Gauge flux
  1. In code space, stabilizers are , so total gauge flux (of either color) into volume must be
  1. When there are physical errors, there is a net charge on a volume
    • Redundancy green charge = yellow charge
    • Vertices necessarily have no net charge, even with physical errors
  2. Measurement errors can result in net charge on vertices or mismatch of charge measured at volumes
Physical errors only
Physical and measurement errors
Error correction

Error correction is a two step process:

  1. Validate gauge flux to remove broken loops

    • Identify end points of broken loops and match them up

  2. Correct residual errors to ensure charge on volumes is neutral

    • Identify stabilizer violations and match them up
Single-shot QEC | numerical evidence

QEC step:

  1. Apply channel to each qudit

  2. Compute gauge syndrome

  3. Randomize each gauge outcome with probability

  4. Find recovery operator:

    1. Validate flux (clustering)
    2. Correct errors (clustering)

Error channel:

Boundaries

  • Unlike topological codes, these subsystem codes require boundaries to have logical qudits

  • Our perspective lets us construct boundaries from boundaries of 2D topological models

  • On , macroscopic copies of the 2D code are used to define the gauge operators

Boundaries | Encoded qubits
  • Logical qubits associated with boundary 2D codes
  • Bare logical operators are sheet-like
  • Dressed logicals are boundary string operators
Boundaries

When defined on a cube, we can use the boundaries of the 2D code to define the gauge operators

Summary

  • New perspective on topological subsystem codes

    • Single-shot property arising from interplay of 2D topological order and 3D geometry

  • This perspective provides a natural generalization to any abelian group/(untwisted) abelian QD anyon model

    • Includes boundaries and logical operators
Summary

  • Beyond Pauli case?

    • Currently working on semion version. Seems to need a different geometry
    • Non-abelian case?
    • General string-net models?

  • Can we fit the gauge color code into this framework?

    • The split between Gauss law and stabilizers is not as clear
    • What is the correct notion of equivalence for subsystem codes?

Any questions?

arXiv:2305.06365

Slides available at jcbridgeman.github.io

site stats